由于有时候客户生命周期很难直观获得，在计算生命周期时，我们可以使用如下公式：

LT = 1 / Customer Churn Rate

其中，Customer Churn Rate为客户的流失率，一般通过当期（月度或年度）流失的客户数/总客户数得来。

很多细心的读者对此提出了疑问，凭什么“客户生命周期就是流失率的倒数”呢？

Prash Majmudar有个帖子很好的解释了这个问题。本文就是对这个帖子的整理和发展。

客户流失和生命周期的定义

首先，解释一下客户流失到底是什么意思。我们可以将客户流失定义为一年结束时客户离开我们的概率。例如，如果客户流失率是50%，那么年底时，客户流失的概率和抛硬币猜正反面是类似的：正面客户会流失，反面客户会续约。当然，我们可以选择任何时间长度来考虑这个问题，不一定非要一年，例如，可以统计每天、每周或每月的客户流失情况。

显然50%的流失率高得离谱，现在我们假设流失率为20%。我们可以得到一年后，客户流失的概率P等于：

P（Y=1）= 0.2

我们还可以问这样一个问题：客户两年后流失的概率是多少？在这种情况下，他们第1年续约(续约概率为0.8)，但在第2年年底流失了。所以2年后客户流失的概率是:

P（Y=2）=0.8 * 0.2 = 0.16

因此，两年后客户流失的概率为0.16或16%。同样我们可以问一个客户在3年甚至10年(9次续约后流失)后流失的概率是多少?

P（Y=3）=0.8*0.8*0.2=0.128

P（Y=10）=0.8*0.8*0.8*0.8*0.8*0.8*0.8*0.8*0.8*0.2=0.027

我们计算出，一个客户3年后流失的概率为0.128，或者说，该客户拥有3年的客户生命周期。同样，我们也可以说客户有2.7%的概率拥有10年的生命周期。

客户流失的简单模型：几何分布

第10年的那个计算写起来有点乏味，我们可以把它写得更一般些:

P（Y=y）= p(1-p)y-1 y=1,2,3,....,10

p为客户流失率，在0和1之间。

我们发现，上面这个方程描述的就是典型的几何分布，这是一种离散型概率分布，用于模拟直到一个事件发生(在我们的例子中，是指客户流失)，某个试验进行的次数(在我们的例子中，试验是客户决定续约或流失的连续年份)的概率分布。

为了说明它与我们之前的例子之间的关系，对于20%的流失率，p=0.2，带入公式:

P（Y=y）= p(1-p)y-1

得到，P（Y=y）=0.2*(1-0.2)^y-1，化简得到 P（Y=y）=0.2 * 0.8^y-1

我们可以画出每年的这个概率，直观地展示客户在第1、2、3、4……年之后流失的概率。我们还可以绘制出p=0.1时的情况，也就是说，在流失率为10%的情况下的客户流失概率情况:

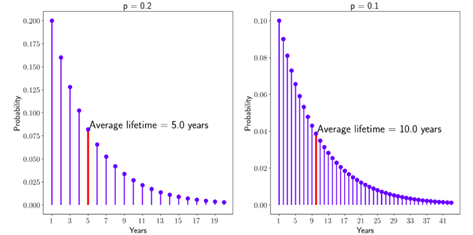
在左边的图中，正如预期的那样，我们可以看到一年后的流失概率是20%，两年后流失的概率是16%——正如我们之前计算的那样。留住一个客户5年的概率（也就是4次续约后流失的概率）只有8.2%，然而这为何恰巧是我们估算的客户平均生命周期呢？

我们可以通过计算每年做出的加权贡献的总和来计算平均客户寿命:

平均生命周期 = P（Y=1）*1 + P（Y=2）*2 + P（Y=3）*3...

=0.2*1 + 0.16*2 + 0.128*3...

这个加和可以永远持续下去，我们可以画出它是如何随着每一个贡献而增长的:

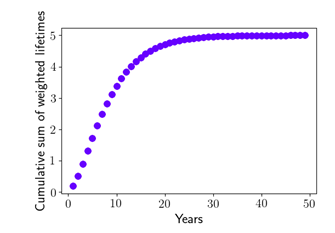
从上图形象化角度我们可以发现，在流失率为0.2的情况下，客户平均生命周期极限为5年。

在Prash Majmudar的文章中，他继续进行了解释和证明。其实，在证明了客户流失率属于几何分布之后，我们就可以利用几何分布的数学期望得到答案了。

几何分布的数学期望

几何分布具有如下规律：

为得到1次成功事件（概率为p）而进行n次伯努利试验，所进行的试验次数X的数学期望如下：

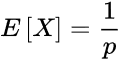
怎么理解呢？

假如，你表白你的暗恋对象，如果你每次表白的成功概率是60%，同时你也符合几何分布的特点，所以表白次数的数学期望E(x)=1/p=1/0.6=1.67。你可以期望自己表白1.67次（约等于2次），就会成功。

同理，如果你的客户流失率为20%，同时它也符合几何分布的特点，所以E(x)=1/p=1/0.2=5。也就是说平均试验5次，客户流失就会发生，即客户的平均生命周期为5年。至此，客户平均生命周期是流失率的倒数就很容易理解了，即Customer Average Life Time = 1 / Customer Churn Rate

推荐阅读：